Preparing simulation dataset 🔗
This study simulated time-to-event data from Cox regression with use-specified coefficients. The harzard model is given by: $$ h(t|X)= e^{(\alpha+\beta X)}= e^{\alpha} * e^{(\beta X)} = h_0(t)*e^{\beta X}$$ where:
- X is the covariate vector
\(\alpha\)is the intercept\(\beta\)is the coefficients vector- h(t|X)is the hazard function at time t given X -
\(h_0(t)\)is the baseline hazard
The survival function of the cox proportional hazards model is then given by:
$$\begin{aligned} S(t|X) &= e^{H(t)} \text{ (see appendix) } \\ &= e^{ \int_0^t h(t|X)} \\ &= e^{ \int_0^t h_0(t)dt*e^{\beta*X}}\\ &= e^{ H_0(t)*e^{\beta*X}} \end{aligned}$$
Then the distribution function of Cox proportional hazards model is:
$$ F(t|X) = 1 - S(t|X) = 1 - e^{ H_0(t)*e^{\beta X}} $$ t|X ~ F,U = F(t|X) is uniform(0,1), 1-U = 1- F(t|X) = S(t|X) is also uniform(0,1), that is:
$$U = e^{ H_0(t)*e^{\beta*X}} \text{~} U(0,1)$$
Then, $$ T = H_0^{-1}[-log(U)e^{(-\beta X)}]$$
Assumptions:
- Survival time follows exponetial/weibull/Gompertz distribution
- Censoring time follows exponential distribution

#' Simulate a survival data set
#'
#' @param nsample total number of observations
#' @param varnum total number of covariates
#' @param dist distribution of baseline hazard function
#' @param lambda scale parameter of the distribution
#' @param rho shape parameter of the distribution
#' @param beta pre-specified effect size of covariates
#' @param crate rate parameter of the exponential distribution
#' @param cor logical; whether consider the correlation between covariates
#' @param seed
#'
#' @return a dataframe; time, status, covariates
#' @export
#' @examples
#'library(survival)
#'dat <- sim_survdat_f(nsample =1000, varnum = 25,dist='g',lambda=0.01, rho=1, beta=c(2.3,0.3,0.4), crate=0.001,cor=TRUE,seed=20231106)
#'fit <- survival::coxph(Surv(time, status) ~ X1+X3+X1*X3, data=dat)
sim_survdat_f <- function(nsample = 100,
varnum =25,
dist = 'w',
lambda = 0.01,
rho = 1,
beta=NA,
crate = 0.001,
cor=TRUE,
seed = 20231106,
...)
{
library(pacman)
pacman::p_load(tidyverse)
Sigma=matrix(rep(0,varnum), nrow=varnum, ncol=varnum, byrow=F)
for(i in 1:varnum){Sigma[i,i]=10}
# Correlation Settings
if(cor){
Sigma[1,2]=3;Sigma[1,3]=3;Sigma[1,4]=6;Sigma[1,5]=6
Sigma[2,1]=3;Sigma[3,1]=3;Sigma[4,1]=6;Sigma[5,1]=6
Sigma[2,3]=3;Sigma[2,4]=2;Sigma[2,5]=1
Sigma[3,2]=3;Sigma[4,2]=2;Sigma[5,2]=1
Sigma[3,4]=2;Sigma[3,5]=1
Sigma[4,3]=2;Sigma[5,3]=1
Sigma[4,5]=1
Sigma[5,4]=1
}
set.seed(seed)
covar_df <- data.frame(MASS::mvrnorm(n = nsample, rep(0, varnum), Sigma/10))
beta_df <- matrix(rep(beta,each = nsample),ncol = length(beta)) %>% data.frame()
modelvar_df <- covar_df %>% select(X1,X2,X3,X4,X5) %>% mutate(X1_X2 = X1*X2,X3_X4=X3*X4)
Z <- apply((beta_df*modelvar_df), 1,sum) %>% unlist()## element-wise product of two data frames
# X1 <- covar_df$X1
# X3 <- covar_df$X3
# Z = beta[1]*X1+beta[2]*X3+beta[3]*X1*X3
U <- runif(n=nsample)
if(dist == 'e'){
time <- (- log(U) / (lambda * exp(Z)))
}
if(dist == 'w'){
time <- (- log(U) / (lambda * exp(Z)))^(1 / rho)
}
if(dist =='g'){
nd_term = ( (rho * log(U)) / (lambda * exp(Z)))
time <-(1/rho) * log(1- nd_term)
}
# censoring times
C <- rexp(n=nsample, rate=crate)
# follow-up times and event indicators
status <- as.numeric(time <= C)
time <- pmin(time, C) ## over-write time variable, compare between time and censor time
# data set
data.frame(time=time,
status=status,
covar_df)
}
#
# set.seed(1234)
# betaHat <- rep(NA, 1e3)
# for(k in 1:1e3)
# {
# dat <- sim_survdat_f(varnum = 25,nsample =1000, lambda=0.01, rho=1, beta=c(2.3,0.3,0.4), crate=0.001,cor=TRUE,seed=20231106)
# fit <- coxph(Surv(time, status) ~ X1+X3+X1*X3, data=dat)
# betaHat[k] <- fit$coef[[2]]
# }
# mean(betaHat)
Bootstrap sampling 🔗

#' Generating bootstrap sample datasets
#'
#' @param df working dataset,simulated or real data collected
#' @param nboot number of bootstrap datasets
#' @param boot_ft number of features in each bootstrap dataset
#' @param seed random seed
#'
#' @return a list, size = nboot, each element is a dataframe
#' @export
#'
#' @examples
#'library(survival)
#'dat <- sim_survdat_f(nsample =1000, varnum = 25,dist='g',lambda=0.01, rho=1, beta=c(2.3,0.3,0.4), crate=0.001,cor=TRUE,seed=20231106)
#'fit <- survival::coxph(Surv(time, status) ~ X1+X3+X1*X3, data=dat)
#' boot_lst <- boot_f(df = ,nboot = 100,boot_ft = 5,seed = 20231106)
boot_f <- function(df = NA,
nboot = 100,
boot_ft = 5,
seed = 20231106) {
## get the feature names in df total features
tot_ft <- df %>% select(matches("^X\\d+$")) %>%
# starts_with("X") # ^ start sign;
# $ end of a string, d+ one or more digital
## This may be problematic if df is not generated from sim_surv_f
colnames()
set.seed(seed)
boot_lst <- lapply(1:nboot, function(x) {
### sample boot_ft from tot_ft
boot_feature <- sample(tot_ft, boot_ft, replace = FALSE) %>%
naturalsort::naturalsort()
### sample nrow(df) people from df with replacement;
boot_sample <- df %>%
#### sample status = 1
filter(status == 1) %>%
sample_n(size = nrow(.), replace = TRUE) %>%
bind_rows(df %>% filter(status == 0) %>%
#### sample status = 0
sample_n(size = nrow(.), replace = TRUE)) %>%
select(time, status, all_of(boot_feature))
})
return(boot_lst)
}
Modelling 🔗
Applied Cox regression with penalty (Lasso or Ridge)to fit the data.
library(survival)
#source("R/01_simulate_survival_data.R")
#source("R/02_bootstrap_datasets.R")
dat <- sim_survdat_f(nsample = 1000, varnum = 25, dist = "g", lambda = 0.01, rho = 1, beta = c(1.8,0.5,0.4,-0.4,0.45,0.6,-0.6), crate = 0.001, cor = TRUE, seed = 20231106)
DT::datatable(dat, filter='top', editable = 'cell',extensions = 'Buttons',
options = list(dom = 'Blfrtip',
scrollX = TRUE,
scrollY = TRUE,
buttons = c('copy', 'csv', 'excel', 'pdf', 'print'),
lengthMenu = list(c(5,25,50,100,-1),
c(5,25,50,100,"All")),
columnDefs = list(list(className = 'dt-center', targets = "_all"))
))
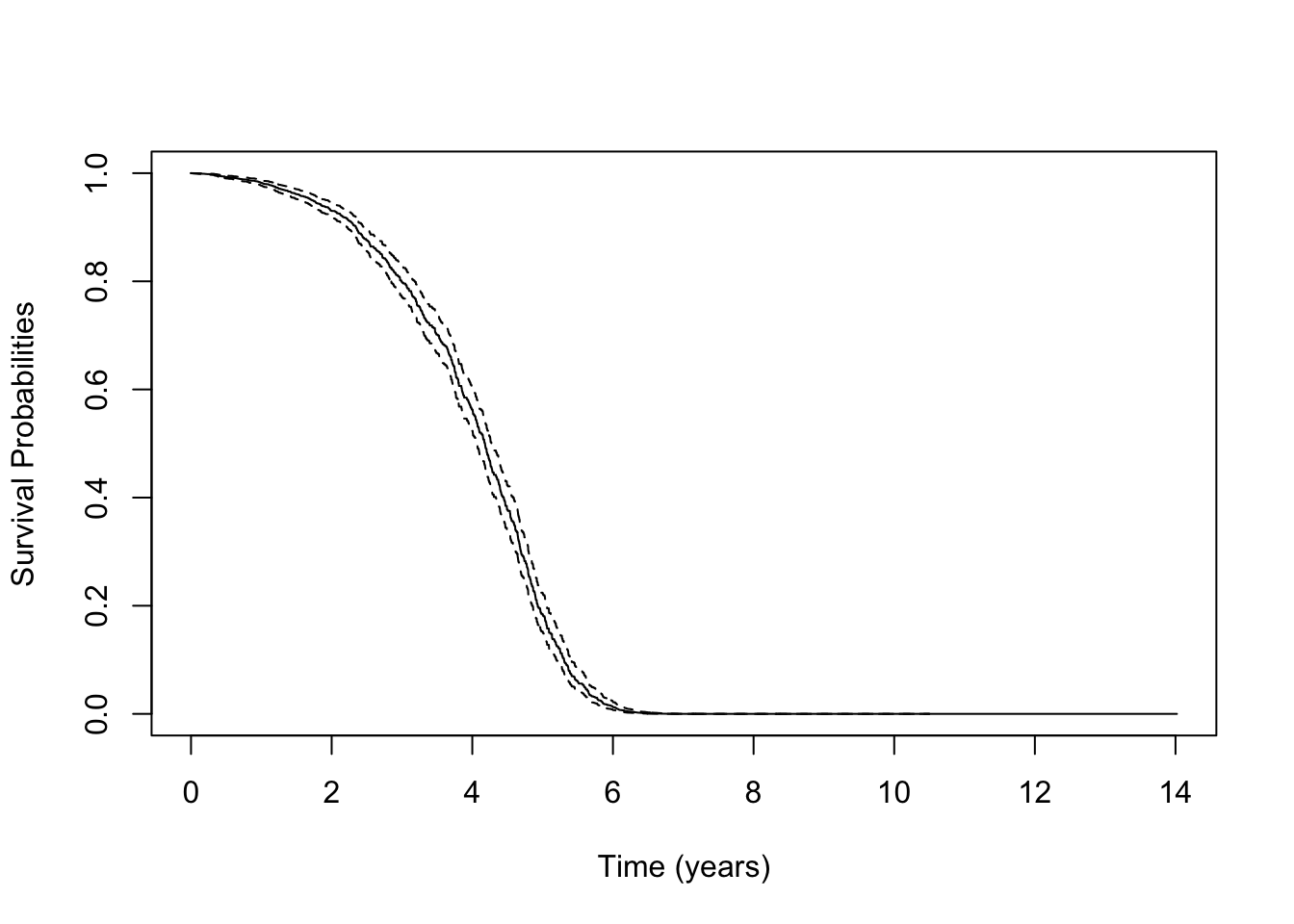
fit <- survival::coxph(Surv(time, status) ~ X1 + X2 + X3 + X4+ X5+X1*X2+X3*X4, data = dat)
plot(survfit(fit), xlab = 'Time (years)', ylab = 'Survival Probabilities')
fit
## Call:
## survival::coxph(formula = Surv(time, status) ~ X1 + X2 + X3 +
## X4 + X5 + X1 * X2 + X3 * X4, data = dat)
##
## coef exp(coef) se(coef) z p
## X1 1.79679 6.03028 0.07253 24.772 < 2e-16
## X2 0.49987 1.64850 0.03846 12.998 < 2e-16
## X3 0.41992 1.52184 0.03642 11.528 < 2e-16
## X4 -0.36466 0.69444 0.04541 -8.031 9.66e-16
## X5 0.40368 1.49732 0.04905 8.230 < 2e-16
## X1:X2 0.66468 1.94387 0.03650 18.213 < 2e-16
## X3:X4 -0.62706 0.53416 0.03724 -16.837 < 2e-16
##
## Likelihood ratio test=1638 on 7 df, p=< 2.2e-16
## n= 1000, number of events= 995
boot_lst <- boot_f(
df = dat,
nboot = 100,
boot_ft = 5,
seed = 20231106
)
#boot_df <- boot_lst[[1]]
pacman::p_load(glmnet)
HDSI_model_f <- function(boot_df = NA,
method = "lasso") {
library(pacman)
pacman::p_load(glmnet)
### x input in cv.glmnet
y <- "survival::Surv(time,status)"
## f=stats::as.formula(paste(y," ~ .*.*."))
f <- stats::as.formula(paste(y, " ~ .*.")) ## pair-wise interaction
X <- stats::model.matrix(f, boot_df)[, -1]
### y input in cv.glmnet
time <- boot_df$time
status <- boot_df$status
Y <- Surv(boot_df$time, boot_df$status)
if (method == "lasso") {
cv_fit <- glmnet::cv.glmnet(
x = X, y = Y, alpha = 1,
standardize = F, family = "cox", nfolds = 5
)
lambda.1se <- cv_fit$lambda.1se
lambda.min <- cv_fit$lambda.min
model_fit <- glmnet::glmnet(x = X, y = Y, lambda = lambda.1se, alpha = 0, standardize = F, family = "cox")
model_coef <- as.matrix(coef(model_fit, s = lambda.1se)) %>%
data.frame() %>%
mutate(varname = rownames(.))
pred <- predict(model_fit, s = lambda.1se, newx = X, type = "link")
model_cindex <- apply(pred, 2, Cindex, y = Y)
model_out <- model_coef %>% mutate(model_cindex = model_cindex)
# y1 = cbind(time = time, status = status)
#
# apply(risk_scores, 2, glmnet::Cindex, y=y1)
}
if (method == "ridge") {
cv_fit <- glmnet::cv.glmnet(
x = X, y = Y, alpha = 0,
standardize = F, family = "cox", nfolds = 5
)
lambda.1se <- cv_fit$lambda.1se
lambda.min <- cv_fit$lambda.min
model_fit <- glmnet::glmnet(x = X, y = Y, lambda = lambda.1se, alpha = 1, standardize = F, family = "cox")
model_coef <- as.matrix(coef(model_fit, s = lambda.1se)) %>%
data.frame() %>%
mutate(varname = rownames(.))
pred <- predict(model_fit, s = lambda.1se, newx = X, type = "link")
model_cindex <- apply(pred, 2, Cindex, y = Y)
model_out <- model_coef %>% mutate(model_cindex = model_cindex)
}
return(model_out)
}
m <- c("lasso", "ridge")
model_out_all <- lapply(1:length(m), function(x) {
lapply(1:length(boot_lst), function(y) {
HDSI_model_f(boot_df = boot_lst[[y]], method = m[[x]])
})
})
tmp <- lapply(1:length(m), function(x) {
## bind B boot sample results into a dataframe
perf_tmp <- model_out_all[[x]] %>% bind_rows()
fe_star <- perf_tmp %>% group_by(model_cindex) %>% summarise(n=n())
### compute min_cindex
min_cindex <- perf_tmp %>%
group_by(varname) %>%
summarise(min_cindex = min(model_cindex)) %>%
mutate(
miu_min_cindex = mean(min_cindex),
# sigma_min_cindex = sqrt(mean((min_cindex - miu_min_cindex)^2) / (fe_star$n %>% unique() - 1)),
sd_min_cindex = sd(min_cindex),
Rf = 2, ## hyperparameter
include_yn = min_cindex > (miu_min_cindex + Rf * sd_min_cindex)
)
### compute coef estimate and CI
beta_quantile <- perf_tmp %>%
group_by(varname) %>%
mutate(quantile = 0.05) %>% ## quantile is a hyperparameter
summarise(
qtl = 0.05,
beta_hat = mean(X1),
qtl_lower = quantile(X1, probs = qtl/2),
qtl_upper = quantile(X1, probs = 1 - (qtl /2) ),
include0_yn = !(((qtl_lower <= 0) & (0 <= qtl_upper)) | ((qtl_upper <= 0) & (0 <= qtl_lower)))
)
### join beta and cindex in a dataframe; filter selected features
perf <- full_join(beta_quantile, min_cindex, by = "varname") %>%
filter(include0_yn == TRUE & include_yn == TRUE)
### adding back main effect if only interaction terms are selected
included_inter <- perf$varname[str_detect(perf$varname, ":")] ## detect interaction terms
## detect main effect terms from interaction
included_inter1 <- stringr::str_split(included_inter, ":") %>% unlist()
## final selected features
included_fe <- c(perf$varname, included_inter1) %>% unique()
res <- list(perf,included_fe)
res
})
tmp11 <- tmp[[1]][[1]] %>% data.frame()
tmp21 <- tmp[[2]][[1]] %>% data.frame()
DT::datatable(tmp11, filter='top', editable = 'cell',extensions = 'Buttons',
options = list(dom = 'Blfrtip',
scrollX = TRUE,
scrollY = TRUE,
buttons = c('copy', 'csv', 'excel', 'pdf', 'print'),
lengthMenu = list(c(5,25,50,100,-1),
c(5,25,50,100,"All")),
columnDefs = list(list(className = 'dt-center', targets = "_all"))
))
DT::datatable(tmp21, filter='top', editable = 'cell',extensions = 'Buttons',
options = list(dom = 'Blfrtip',
scrollX = TRUE,
scrollY = TRUE,
buttons = c('copy', 'csv', 'excel', 'pdf', 'print'),
lengthMenu = list(c(5,25,50,100,-1),
c(5,25,50,100,"All")),
columnDefs = list(list(className = 'dt-center', targets = "_all"))
))
# var_freq <- stringr::str_split(min_cindex$varname,":") %>% unlist() %>% table() %>% data.frame()
Survival fundation 🔗
- Survival function: the probability of survival times T larger than t
$$S(t) = P(T>=t) = 1-P(T<t) = 1-F(t)$$
- Hazard function : the probability of 「failure」at time t
\(\begin{aligned} h(t) &= lim_{\delta_t\rightarrow0}\frac{P(t< T <= t+\delta_t|T>t)}{\delta_t} \\ &= lim_{\delta_t\rightarrow0}\frac{P(t< T <= t+\delta_t,T>t)}{\delta_t * P(T>t)} \text{ [write out the conditional probability ]}\\ &= lim_{\delta_t\rightarrow0}\frac{P(t< T <= t+\delta_t)}{\delta_t * P(T>t)} \text{ [P(t<T<=t+ {\delta_t}) is a subset of P(T>t) ]}\\ &= lim_{\delta_t\rightarrow0}\frac{F(t+\delta_t) -F(t)}{\delta_t * S(t)} \\ &= \frac{f(t)}{S(t)} \\ \end{aligned}\)
- relationships between h(t),S(t)and f(t)
\(\begin{aligned} h(t) &= \frac{f(t)}{S(t)}\\ &= \frac{f(t)}{1-F(t)}\\ &= -\frac{d}{dt}ln(1-F(t))\\ &= -\frac{d}{dt}ln(S(t))\\ \end{aligned}\)
\(\begin{aligned} -\frac{d}{dt}ln(S(t)) &= h(t)\\ d (ln(S(t))) &= -h(t)dt\\ ln(S(t)) &= -\int_0^t h(t)dt\\ S(t) &= e^{-H(t)}\\ \end{aligned}\)