- likelihood uncensored pts contribute to survival + hazard; censored pts contribute only to survival –> survival is a function of hazard –> likelihood is a function of hazard;
- Two assumptions: A1. independent censoring (t_tilde indep censoring given covariates) and A2. non-informative censoring (censoring distribution does not involve params of interest, so it can be dropped out from the likelihood)
- continuous time: exp/pois identity. homogeneous Poisson process (for each individual, only count to 1 in survival analysis) P_exp(X>t) = P_pois(N(t)=0) [for pts i, event does not happen till time t, exponential PDF(param=1/lambda) capture the wait time till next event in poisson process, taht is, the wait time between two events is exponential distributed]. This is the simplest survival model: constant hazard model. survival = e^(-t*lambda) = e^(-t*lambda0exp(beta*x)) [first equality is from the CDF of exponential dist; second equality is from the specified model]; Weibull model. 很好理解:就是一个counting process,一直数,把所有数据都aggregated起来。所以用exp(rate=lambda)和N(tao)-N(0)=Poissosn(lambda*tao)来写likelihood是一样的
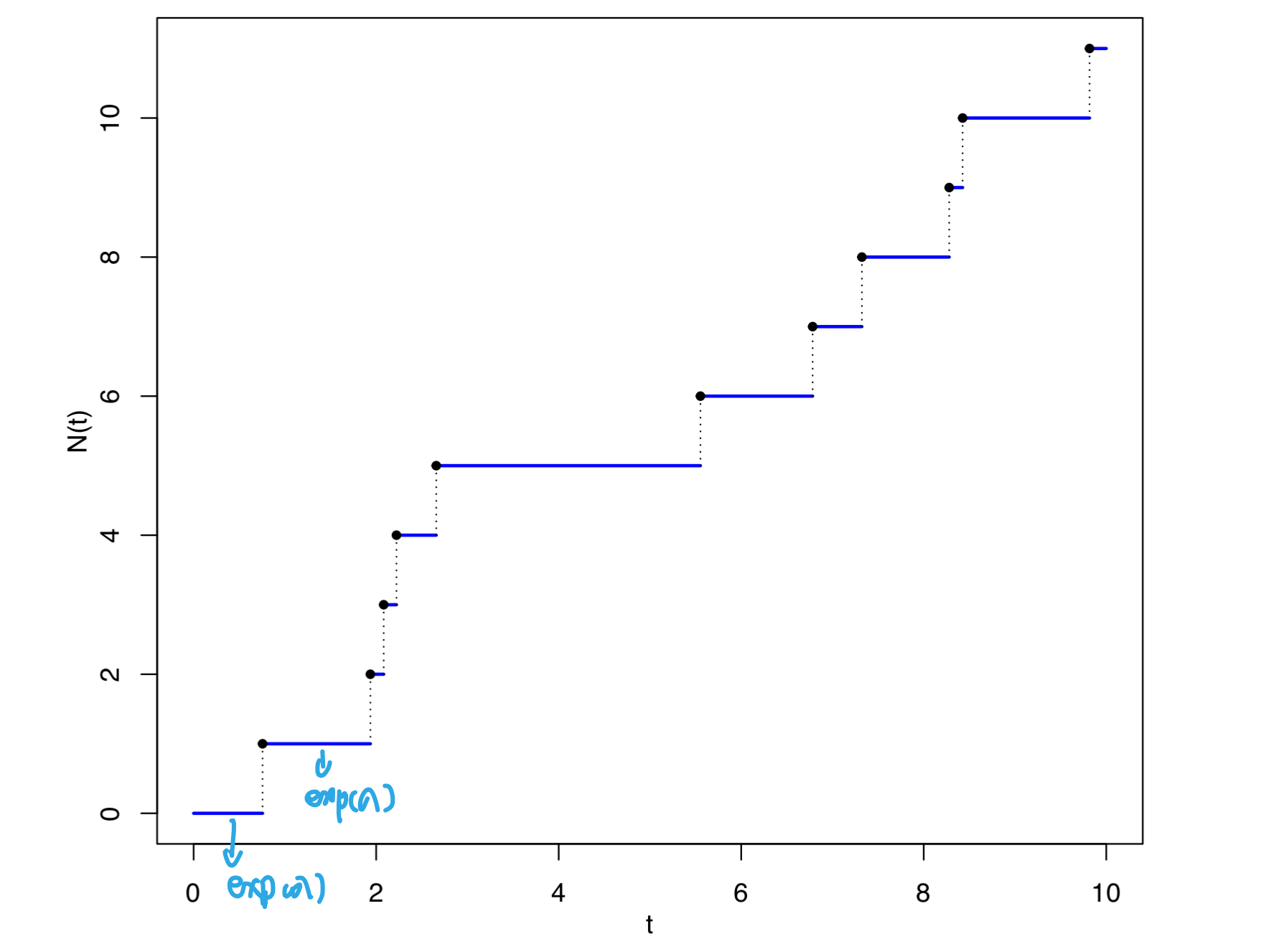
side note: (memorylessness : Pr(T>25∣T>15)=Pr(T>10):在你已经等了15分钟的情况下,再等10分钟以上的概率(即等总共25分钟以上的概率)与从一开始就等10分钟以上的概率是相同的 这是可以理解的; geometric: Pr(X>n+m∣X>=n)=Pr(X>m) support {0,1,2} 另外一种parameterization方法为Pr(X>n+m∣X>n)=Pr(X>m) support {1,2,3} )